UoPeopleでCollege Algebra(大学代数学)を修了した振り返り
学費無料のオンライン大学、University of the PeopleでMATH1201-College Algebra(大学代数学)を履修したのでその感想を書きます。
前回までのあらすじ
- コンピューターサイエンスの学位(学士)を取るために、University of the Peopleという学費無料の米国オンライン大学に入学してみたよ。
- 英語の学力要件はパスできたけど、正式な学部生(Degree-seeking student)になるためには、2つ以上の基礎コースを修了する必要があるよ。
- 1つ目の基礎コースOnline Education Strategiesは無事終了したよ。
- コロナ禍で在宅勤務 with kidsの最中だったからクソしんどかったよ。
- 2つ目の基礎コースはCollege Algebra(大学代数学)を受けることにしたよ。
Motivation
数学に対してはもっっっのすごく苦手意識があったんですが、その分克服したい分野でもありました。
高校数学は数1Aと数2Bの序盤という最低限の範囲しかやっておらず、大学でも数学の知識を全然使わなかったので、
「微分積分やったことない」
「虚数 って 何」
「この左上に数字があるn√xって何」
「因数分解の公式とか忘れた」
「式変形のやり方うろ覚え」
っていうレベルでした😇
アルゴリズムの学習には何度かトライしたりもするんですが、やはり数学の基礎知識がなさすぎて躓きまくるんですよ。
競プロの解説やアルゴリズムの書籍なんかを読んでると当然数式や用語がバンバン出て来ますよね。
「このf(x)ってなに…。(ぐぐる)あ、関数のことなんですね…」
「漸化式とか行列を使って解くとか言われてもよくわからん…」
「意味のわからない数式が多すぎてぐぐるのも一苦労」
というレベル。
これは中学数学・高校数学から腰を据えてやり直した方がいいやつだ…。
でも自分一人だと継続的にモチベーションを保つ出る自信がない…。
ということでCollege Algebraは楽しみなコースの一つでした。
コース内容
College Algebra(大学代数学)って名前は大層ですが、以下の通り高校数学+アルファという内容です。
- 関数、写像、定義域、値域
- 1次関数・二次関数
- べき関数、多項式関数、有理関数
- 組立除法
- 有理根の定理、因数定理、剰余の定理、デカルトの符号法則
- 合成関数、逆関数
- 指数関数、対数関数
- 連立一次方程式、非線形連立方程式
- ガウスの消去法
- 三角法
- 周期関数、奇関数、偶関数、三角関数の加法定理、二倍角の定理
- 複素数
- 極座標
- ド・モアブルの定理
少し古いですがシラバスがこちらで見れます。
高校数学を数Ⅲ数Cとかまでやった人は楽勝なんじゃないでしょうか。多分。
ただ、高校数学では扱われてない内容も含まれています。
また、グラフの分析が重視されていたり、現実世界に数学の考え方を適用させる練習を何度もやるのでより実践的なのではと思います。
参考になったサイトやツールたち
関数、写像、関係についての解説
Unit1は「関数」や「関係」の定義から始まります。
高校数学の範囲ではないので日本語でのわかりやすい資料がネットでは探しづらく苦労しました。
英語での数学の基礎的な用語もわからない中、テキストには
「function」「relation」「component」「element」「pair」「set」など一般的な単語がどんどん出てくるので
「これは日本語の数学用語だと何に該当するんだ??」
「そのまま一般的な用語に訳していいのか??」
と戸惑いました。
そんな中、以下の資料は「関数」や「関係」の違いを理解するのにとても助けになりました。
「Determining Whether a Relation Represents a Function」について日本語で解説している資料がほしい…って「関数 関係」「関数 定義域 値域」とかでぐぐってたんだけどコレジャナイ感じで、ふと「写像 関係」で検索したらようやくドンピシャなのがでてきたよ…😇https://t.co/RAqMi8HUAU
— えんぴつ (@empitsu88) 2020年6月19日
ネイピア数の解説
Unit 5のExponential and Logarithmic Functionsは今回最も苦労した単元の中の一つです。
なんせテキスト約100ページの範囲を一週間でこなす必要があります😇
以下はUnit5 Reading Assignment(課題図書)の範囲です。
もちろんこれを読む以外にも練習問題を解いたり動画教材を見たり課題x3を提出したりする必要があります。一週間で。

改めてAlgebraの今週の範囲やべえな…指数法則から学び直してる状態なのに一週間で
— えんぴつ (@empitsu88) 2020年7月19日
指数関数・対数関数、方程式、自然対数・常用対数の応用、指数的対数的成長・減衰、複利式、半減期の計算、放射性炭素年代測定、指数回帰、ロジスティック回帰までやるの無茶すぎん?😇#Algebra #UoPeople
また、指数的成長・減衰(↓こういうやつ)の公式を活用する問題がたくさん出てくるのですが、解説が日本語でなかなか見つけられなくて死にました。
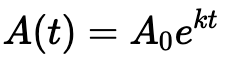
Exponential Growthの関数𝑦=𝐴_0𝑒^{𝑘𝑡}の日本語の解説少なすぎない…?
— えんぴつ (@empitsu88) 2020年7月19日
「指数関数的成長」でぐぐるとビジネスのポエムばっかりでてくるんだが、ググり方が間違ってるのか…?
ネイピア数、しれっと登場したが調べれば調べるほど何もわからない…「微分しても変わらない」と言われてもまず微分積分が理解できてないワイhttps://t.co/6FYFzxKHyR
— えんぴつ (@empitsu88) 2020年7月19日
ネイピア数eに関しては以下の記事が参考になりました。
ちなみにネイピア数はテキストではEuler’s constantと書かれています。
欧米ではネイピア数のことをEuler’s constantとかEuler's numberと呼ぶようです。
日本語で言うオイラーの定数 γ やオイラー数列とは異なるので注意してください。
対数を普通の電卓だけで計算する方法
Self-Quizや課題では、自然対数や暗算では計算できない対数(log_2(5)など)が入った値を求める問題が時折出てきます。
関数電卓やOnline Calcuratorで計算すれば済むのですが、最終試験では普通の電卓しか使ってはいけません。
もちろん関数電卓もスマートフォンもOnline Calcuratorも使用はNGです。
「えっ最終試験ではこういうのどうやって計算するんだ…小数点第一か第二くらいまではわからないと答えずれる…」
と絶望していましたが調べると電卓で計算する方法がありました。
こちらの方法を使えば、自然対数もlog_2(5)なども電卓だけで近似値を計算できます。
また、常用対数や底が整数の対数ならば以下の方法も使えます。
英語の数学用語まとめ
最初の頃は
「えっrangeってここでは”値域”って訳すの」
「powerって”力”じゃなくて”冪乗”なの」
「productって”製品”じゃなくて”かけ算の積”なの」
「coordinateって”調整する”じゃなくて”座標”なの」
みたいな状態だったので以下のようなまとめが大変参考になりました。
高校留学で使う英語の数学用語まとめ│海外留学の情報・準備なら「留スタ」
数学用語 英語 一覧(Mathematics Terminology) | ゆう@アメリカ生活終了→英語勉強
ただ最初の一週間で式変形の過程を英語で説明するくらいまではできるようになる(やらざるを得ない)ので、
基本的な語彙を覚えあとは、「piecewise 数学」「rational root とは」などでぐぐったほうが日訳・英訳を調べるには早いです。
#Algebra #UoPeople
— えんぴつ (@empitsu88) 2020年7月18日
1週目 中学/高校数学ろくに覚えてないやつが来る場所じゃなかった死んだ
2週目 基本的な数学英単語は大体覚えたもん!式の変形の仕方も思い出したもん!
3週目 有理関数めんどい出題範囲広すぎ死んだ
4週目 なにこれ楽勝
5週目 テキストの範囲100ページあって死んだ👈今ココ
Youtubeチャンネル「トライイット」「ヨビノリ」
トライイットと予備校のノリで学ぶ「大学の数学・物理」(ヨビノリ)の動画には本当にお世話になりました。
特にトライイットは数1〜3まで全部解説と動画が揃ってて本当に神です。
コースに慣れてからは
該当の単元を範囲を確認する→トライイットの該当の動画を見る→テキストを読む
という流れで進めていました。
とりあえずこの週末でtry itの指数、対数、極限、ネイピア数に関する動画33本見たから前提知識は大丈夫なはずだ(ヽ´ω`)#UoPeople #Algebra
— えんぴつ (@empitsu88) 2020年7月19日
ただAlgebraの各Unitは中学数学〜高校数学Ⅰ,Ⅱ,Ⅲの範囲が混ざっていたり、高校数学で扱ってない内容が入ってることも多いため、
全く予備知識がない状態だと「今回の範囲が中学数学・高校数学のどの単元に値するのか。そもそも高校数学の範囲ではないのか」を調べるのにまず時間がかかったりします。
例えば、Unit 3: Polynomialsは以下のように範囲が広く、トライイットからずばり該当している動画を探すのは少々面倒でした。

Unit3で参考になったトライイットの動画:
「複素数と方程式」の勉強法のわからないを5分で解決 | 映像授業のTry IT (トライイット)
「整式の割り算」の勉強法のわからないを5分で解決 | 映像授業のTry IT (トライイット)
【高校数学Ⅲ】「グラフのかき方(2)」(問題編) | 映像授業のTry IT (トライイット)
また、Unit 6: Systems of Equationsでの「ガウスの消去法」(別名:掃き出し法)は高校数学では扱われておらずトライイットにも該当の動画はなかったのですが、ヨビノリの以下の動画が参考になりました。
【大学数学】線形代数入門⑤(連立方程式:掃き出し法)【線形代数】
解き方がわからない時の味方、Wolfram Alpha
Wolfram Alphaは数式を入れると計算してくれる無料のサービスです。
Wolfram|Alpha: Computational Intelligence
課金すると途中の計算式も出してくれます。
「この問題、どうしてこの答えになるの?どうしてこう変形できるの?」って時に助かりました。
何故ならテキストの演習問題には解説は載っていないからです。
そして何故か奇数番号の問題には解答すらありません…。
ただ、最終試験の時は普通の電卓以外使えないので、頼りすぎるのは禁物です。
グラフ計算機 DesmosとGeoGebra
Algebraではグラフを描く課題がでてきます。
方程式を書くとそれをグラフ化してくれるDesmosやGeoGebraというサービスにはお世話になりました。
数式はどうやって書いて提出していたか
課題で数式を書いて提出するときに使っていた方法を紹介します。
TeX記法
MoodleでのWYSIWYGエディタでは「Equation Editor」のボタンを選択するとTeX記法で数式が挿入できます。

が、Macではプレビュー機能がバグってて全然使えませんでした。
なので以下のページのリアルタイムプレビューにはお世話になりました…。
こちらのサイト作ったTeX記法をコピペもしくはスクショを取って画像を貼り付けていました。
ただ数式すべてをTeXで書いているとめちゃくちゃ時間がかかるため、
結局は後述の「プレーンテキスト」だけで書いて済ますことが最も多かったです。
行列式やpiecewise functionなどテキストだと表現しづらい数式でのみTeXを使っていました。
Google Docの「数式を挿入」
Google Docでも数式を挿入できます。
ドキュメントで計算式を使用する - パソコン - ドキュメント エディタ ヘルプ
ただ、.docxへ保存すると数式は消えてしまったので注意してください。
.pdfなら大丈夫でした。
この方法を使ったときはドキュメントを.pdf化して添付、
更にDiscussion Assignmentでは読んでもらいやすくするためにページのスクショを取って画像を貼って提出していました。
プレーンテキスト
テキストのみでも案外なんとかなります。
f(x)=x^3+3x^2+5
とか
f(x)=x^{1/3}
とか。
私のクラスではこの方法を使っている生徒が一番多かったように思います。
全角特殊文字の√や∞、×もMoodleには貼り付けられます。
手書きのノートの写真を取る
手書き(お世辞にも読みやすいとは言えないレベルの文字)のノートをスキャンして提出している人もいます。
私も簡単な図を描く必要があったときはEvernoteアプリやGenius Scanアプリで写真を取ってMoodleに貼り付けて提出していました。
課題について
Discussion Assignment
指示が抽象的で何を書けばよくわからない問題がよく出ます。
混乱しますが、そのunitで学んだことを使って何かしらの回答と考えを書けば8点以上は貰えます。
問題文でぐぐるといろんなサイトがひっかかりますが、 微妙に問題文が変わってたり、文脈が伝わってないせいか的外れな回答が書いてあったりするので気を付けましょう。
勿論、コピペしたり無断で引用すると剽窃になるのでいけません。
Learning Journal
その単元で学んだ内容を振り返るかたちでいくつかの設問に答えます。
毎回10点満点をもらえました。
先生によるとは思いますが、回答に抜けや明らかな誤りがなければ高得点が取れると思います。
Written Assignment
数式を解いたりグラフを書く問題が何問か出ます。
途中式が必須の場合が多いです。
テキストの練習問題を解いていれば大抵のものは解けると思います。
次のUnitで模範解答が発表されるのですが、掲示された解答では微妙に最初の問題文と違っていたり問題番号がずれていたことがありました…。
そのせいでPeer Assessmentで「不正解」とみなされ散々な点数を付けられたこともありました😇
それがなくても無言で低い評価を付けてきたり、全問正解のはずなのに「回答が書いてない」とコメントしてきたりする同級生がおり、毎週のように先生に抗議のメールを送っていました。
模範解答が与えられ、評価基準も比較的明確な数学という教科でもこうも評価がぶれるのは何故なのでしょうね…(遠い目)
今週のAlgebraもなんとか生き残れましたが、発表された模範解答が元々指示されてた問題と番号がずれてたり内容が違ってたりするわ、そのせいで低い点数をつけてくる生徒がいるわで消耗しています😇#UoPeople https://t.co/0gGGhkoRqD
— えんぴつ (@empitsu88) 2020年7月24日
もはや毎週恒例の不当なpeer評価への抗議メールdone😌
— えんぴつ (@empitsu88) 2020年7月30日
模範解答が与えられ、評価基準も比較的明確な数学という教科でもこうも評価がぶれるのは何故なのか…🤔#Algebra #UoPeople
最終試験
試験はProctoredで試験官の監督の下、実施が必要です。
電卓はあったほうがいいです。
Self-quizやGraded quizより難しい問題がいくつか出ましたので、習った公式はテキストをよく読んで復習しておくのが良いです。
学習時間
週に13〜19時間程度を費やしていました。
この学期に受けていたコースはこのAlgebra一つでしたが、自分の時間はほぼすべてこれで潰れていたので、子供がいると週19時間前後がやはり限界だなーと感じています。

最終成績
最終成績は89.0でLetter GradeとしてはB+、GPAとしては3.33でした。

あと1点あればA-だったのでとても悔しい😭
最終試験を受ける前は94/100だったので最終試験で何問か間違えて大きく落としたかたちになりました…。
解き方に自信がなかったものは1問だけだったので、間違えた問題はほとんどケアレスミスや問題の解釈間違いだったのではと思っています。
こういうところに場数や基礎力が出る…。
修了してみての感想
スタート時点の自分のレベルを考えるとだいぶレベルアップできた
Aが取れなかったのは悔しいですが、よく考えたら最初は基本的な語彙も知らず中学数学・高校数学もろくに覚えておらず「虚数って何」とか言ってる状態だったんですよね。
なのに大学数学の初歩の単位(しかも英語)がB以上の成績で取れただけでもよくやった…と思うようにしたいです。
今なら以下のツイートの意味がなんとなく理解できるまでになりました。
半沢直樹「倍返しだ!」
— 佐久間ちゃん迷言Bot (@2_wykipedia) 2020年8月8日
倍沢直樹「半返しだ!」
1/3沢直樹「3倍返しだ!」
x沢直樹「1/x倍返しだ!」
i沢直樹「-i倍返しだ!」
∞沢直樹「返さない」
A沢直樹「(1/det(A))adj(A)倍返しだ!」
√沢直樹「2乗返しだ!」
∫沢直樹「d/dx返しだ!」
sin沢直樹「arcsin返しだ!」
exp沢直樹「log返しだ!」
ファボった数万人の中で「f沢直樹はfの逆演算で返す。fの部分が定数cのときはcをc倍写像と同一視する。これは半=1/2とも半="1/2倍"とも解釈できることに由来している。c=∞の場合は逆がill-definedなので仕方なく極限をとっている。ただし、fは都合の良い定義域で考える。」と分かった人は少なそう。
— 佐久間ちゃん迷言Bot (@2_wykipedia) 2020年8月9日
毎週「私はここで脱落するかもしれん」と思うほど辛かったですが、
中学数学・高校数学を復習しつつ練習問題を解き、課題を提出し、テストを受けるなんて自分一人だけでの自習では絶対にやれない(やらない)ので大学の授業という形で受講できてよかったなと思います。
UoPeople、本当に大変で、苦手なコースは週15時間以上必要になるので自分の時間はほぼこれで潰れる。
— えんぴつ (@empitsu88) 2020年7月18日
でもこうでもしないと中学・高校数学を泣きながら復習しつつ大学数学を理解するなんて自分一人ではやり遂げられなかったと思うので良い機会だなと思う。
大学数学のロードマップは果てしない…
ですが「大学数学」という括りでみると、今回のコースは「入り口を入るか入らないか」くらいの位置づけだと思います。
以下の大学数学ロードマップを見ると「今回のAlgebraって、どれ!?」ってなります😇
「教養数学」の前提となる知識を学んだ、という感じでしょうか…。
Algebraのコース、泣きながらやっていたが、7〜8割は高校数学でカバーされてる内容っぽかったんですよね😇
— えんぴつ (@empitsu88) 2020年8月8日
残りの部分も高校数学をより抽象化したり応用・発展させた内容だったりなので、知識は地続きでありいかに基礎が大事か思い知りましたね…#UoPeople
大学数学のロードマップ ~ 分野一覧と学ぶ順序 https://t.co/FCBNeI7j5r
— えんぴつ (@empitsu88) 2020年8月8日
うーん。Algebraのコース完了目前になって改めてこの図を見ると大海の広さにクラクラしますね…。
今回のコースは代数学の”前提”となる知識と、「教養数学」のあたりをかすったかな…?レベルなのかな😇#UoPeople
今後UoPeopleで学べる数学科目としては
- 「Calculus(微積分)」
- 「Discrete Mathematics(離散数学)」
- 「Introduction to Statistics(統計学)」
- 「Statistical inference (推計統計学)」
などがあるのですが、全部修了してようやく「数学基礎」まででしょうか。
大海は広い…。
そして泣きながら理数系科目の単位を取ったことで、高校数学の範囲(数Ⅰ〜Ⅲ、数A〜C)を全部学んだ人や、CSの学位を持っている人への尊敬の念が一層強まりました。
まだ基礎コースの単位しか取れていないが、Computer Scienceの学部に入ってみて
— えんぴつ (@empitsu88) 2020年8月21日
「単位取るのめちゃくちゃ大変じゃんか!!」
「4年以上の努力をしてCSの学士修士取った人とかどんだけすごいの!?」と自信を失うばかりである。
勉強し始めた結果大海の広さを知るというね…
高校数学の範囲(数Ⅰ〜Ⅲ、数A〜C)を全部学んだ人心の底から尊敬してる
— えんぴつ (@empitsu88) 2020年8月7日
英語で学んだことで多角的に理解できるようになった…気がする
もともと知らなかった知識を外国語で学ぶというのは時間もかかりますし二重で大変ですが、良かった点ももちろんあります。
日本の中学・高校ではあまり聞き慣れないDescartes’ Rule of Signs(デカルトの符号法則)やRational root theorem(有理根定理)を活用したり、三角比を覚える際に便利なニモニック 「SOH CAH TOA」を習えたりします。
日本語と英語両方用語を覚える必要はありますが、ある一つの概念を複数の側面から知ることで理解も深まり記憶にも定着しやすい気がしています。
また、英語での数学表現を覚えることで外資系でのホワイトボードコーディングや技術面接でも役立つ…かも。
三角比、英語だとθの向かいにある辺がOppositeになるのでtanθ=toa =opposite/adjacent とできる。
— えんぴつ (@empitsu88) 2020年8月5日
日本の覚え方みたいに「θを左下に持ってくるとここが底辺なのでtの書き順だと…」とやらなくて済むのは良い。
でもtryitの動画をめっちゃ見たので結局「tは底辺分の高さ」という語呂を使ってしまう😌
無事Degree Seeking Studentになれた
これを修了したことで無事Degree Seeking Studentになれました🎉
これで今まではFoundation Course Studentという扱いだったのですが、正式な学部生になったということです。
Office365や大学のメールアドレスも無料で付与されるとのこと。
また、単位移行の手続きも進められるようになり、私は以前の大学から14コース(単位数で言うと48)が承認されました🎉🎉
単位移行の道のりはまた後日記事にまとめたいと思います。
来期は
以前見送ったCS1101 - Progamming Fundamentals(Python基礎)を受講します。
超基礎ではありますが、初めての「Computer Science」に属する科目なので楽しみです。